I continue this journey in quantum computing with a completly useless, however fundamental, quantum algorithm: The Deutsch Algorithm.

– Hurray, yet another theorical tool that I will never use...

Remember the last time you have to use a Turing machine ? Right. But without Turing Machine, there won't be any of todays modern language.

The Query Model

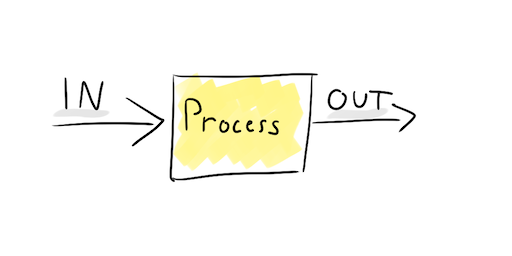
Before talking about quantum algorithm, I have to talk about The Query Model. In traditional computing, you have input data, that goes through a processing, and are transformed into output data:

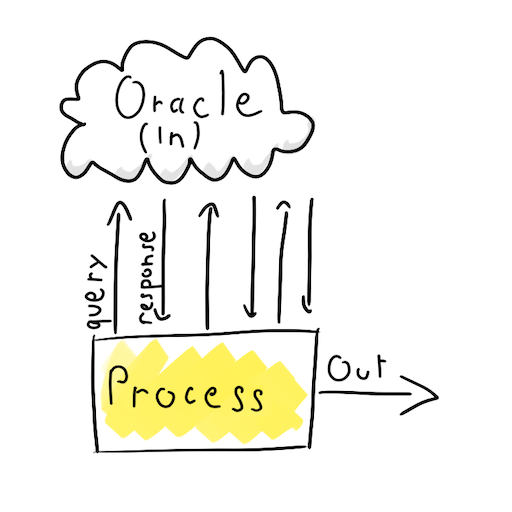
With Query model, we have a black box, called an Oracle. This Oracle know something. For example, the airspeed velocity of an unladen swallow. But you cannot ask it directly "What is the airspeed velocity of an unladen swallow?". You can only ask closed question, like "Is it a European swallow?", or "Is it 10m/s?". And by asking all the possible speed, you will find the information hidden in the oracle.

– Mmm... This look like bruteforce with extra steps.

Yes it is. In classical computing, you will have to ask all the possible values. This specific problem could be optimized using a binary search. This lower the complexity from \(O(n)\) to \(O(log(n))\). But in the end, you will still have to do several queries to the oracle.

Let's formalize this. We have an Oracle function \(f\), taking a binary value and return a binary answer:

For our swallow example, we can encode velocity in uint8 and the oracle return true or false (\(1\) or \(0\)):

Search algorithm would be:

for i in [0, 255]:
   if f(i) == 1
      return i

One can see this algorithm complexity is \(O(N)\). BUT, there is a small subtility. We can consider it \(O(2^n)\), \(n\) being the number of bits used to represent the input. So it has an exponential complexity.

– This makes this algorithm much more scary !

Yes. But when talking about complexity in quantum comlputing, it refer to number of qbits used. To do the parallel with classical algorithm, it's better to compute complexity using number of input bits, and not number of input values.

Now comes the interesting part. In Quantum Computing, as you can put qbits in superposition states, you can ask several questions at the same time, in a single query.

Instead of asking \(f(00000000)?\), \(f(00000001)?\), \(f(00000010)?\), etc... Couldn't we ask \(f(\left| \psi_0 \psi_1 \psi_2 \psi_3 \psi_4 \psi_5 \psi_6 \psi_7 \right>)\) only once where the \(\psi_i\) are all both \(0\) and \(1\) ?

Well, let's try to answer this question.

The Deutsch Problem

We'll try to find if the parity is well respected in a company. This company has only 2 employees, and we want to see if there is one man and one woman in this company. This company, as every companies, is a black box. You can only ask to HR if a given employee is a man or a woman.

– What the hell is this problem ?

Don't blame me, I never found any practical example of Deutsch algorithm, so I'm doing my best !

Anyway, the company is the \(f\) function. There are only 2 employees, so we need one bit to encode the input. Let's take \(0\) for first employee, \(1\) for second one. For a question, the answer has 2 possibilities: man or woman. So we also need a single bit for the answer. Let's take \(0\) for man and \(1\) for woman. We end up with the function:

To know if the parity is respected, we have to ask the question "Is employee \(x\) a man ?" twice. If we know employee \(0\) is a man, maybe the second is a man, maybe a woman. In the end, there are 4 possible cases:

• Both employee are men:

• Both employee are women:

• Employee 0 is a man, and employee 1 is a woman:

• Employee 0 is a woman, and employee 1 is a man:
  $$ f(x) = !x \quad \forall x $$
  NOT \(x\) can be seens as \(1\) XOR \(x\), or \(1 $\oplus\) x\(, $\oplus\) being binary addition without carry.

The Query Gate

One can draw the Query gate of arbitray \(f\) function like this:

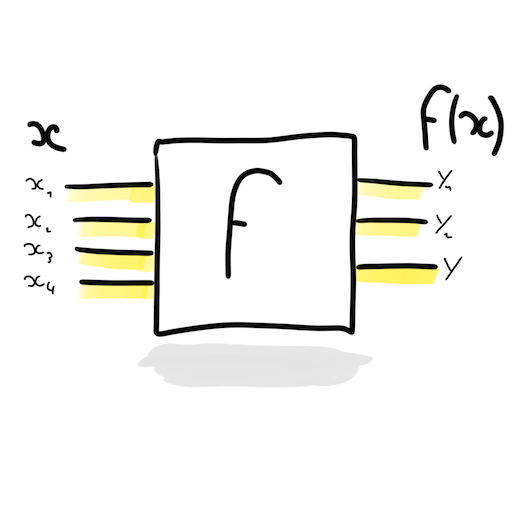
But in quantum computing, this pose a problem. Remember ? Any quantum gate must be invertible (and even unitary). From the gate output, we must be able to find what was the input.

No problem, let's plug the input to the output:

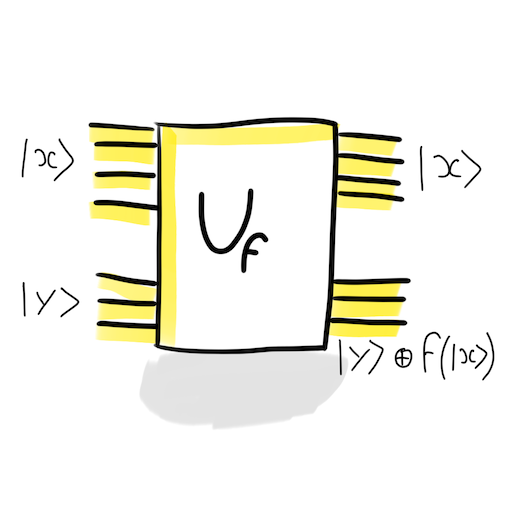
– Wait, why do we need to \(\oplus\) the output ? We already know what was the input with the \(\left| x \right>\) ?

Yes, but tranformation must also be Unitary (whatever this means...). And the \(y \oplus\) makes it unitary for any function \(f\).

For any function \(f\) we can build a quantum gate to query \(f\).

The Deutsch Algorithm

Ladies and gentlemen, this is The Deutsch Algorithm:

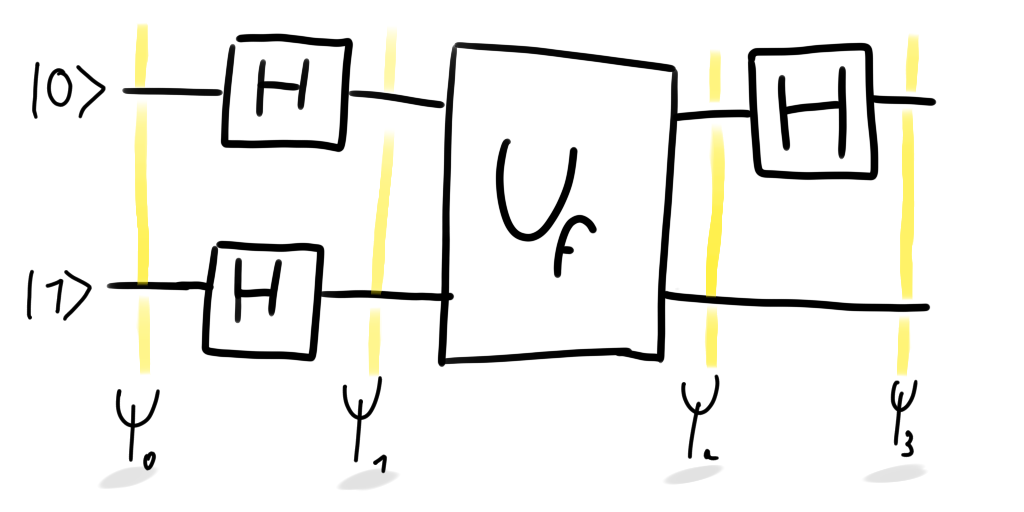
Let's analyse it step by step.

\(\left| \Psi_0 \right>\)

Initial state.

\(\left| \Psi_1 \right>\)

We put the system in superposition state using 2 Hadamard gates:

To really understand what is a superposition state, let write this a bit diferently:

This mean the first qbit \(\left| \psi_1 \right>\) can be \(0\) or \(1\), with probablity \(1/2\). Same for second qbit \(\left| \psi_2 \right>\). (Probability is the square, so \(-1/\sqrt{2}\) still gives probability of \(1/2\))

If we develop this equation, we can also see things differently:

\(\left| \Psi_1 \right>\) is the superposition of states \(\left| 00 \right>\), \(\left| 01 \right>\), \(\left| 10 \right>\), \(\left| 11 \right>\), which is the canonical base of a 2 qbit system. Each states having a probability of \(1/4\) to be measured !

\(\left| \Psi_2 \right>\)

Ok, things get serious. That's where I get I didn't understood anything to Quantum Processing and I decided to start this series of articles.

We have to apply \(U_f\) gate to \(\left| \Psi_1 \right>\). The good news is that \(U_f\) is linear, like any quantum gate. So

Remember, \(U_f(\left| x y \right>) = U_f(\left| x \right> \otimes \left| y \right>) = \left| x \right> \otimes (\left| y \right> \oplus f(\left| x \right>))\).

There were 4 possibilities for \(f\):

• \(f(x) = 0 \quad \forall x\)

• \(f(x) = 1 \quad \forall x\)

• \(f(x) = x \quad \forall x\)

• \(f(x) = !x \quad \forall x\)

Lets compact this a bit:

One notice 2 things. First:

Then:

We end up with

Now, remember a propeties of qbits we have seens previously. Multiplying a qubit by a phase \(e^{i\theta}\) doesn't really matter, whatever \(\theta\). An multiplyin by \(-1\) is multiplyin by a phase \(\Pi\). So we can get rid of the \(\pm\), and factorize into:

– Ohhhhh, it smell like Hadamard's gate here !

Indeed. And we now reach the last step of our algorithm.

\(\left| \Psi_3 \right>\)

Pfew, we're nearly done. Hardest part is behind us. We just have to apply an Hadamard gate on the first qbit:

And we just have to measure the 1st qbit. If \(f\) is constant, its value will be \(0\) with 100% probability. If \(f\) is balanced, it will be \(1\). And we don't care about value of second qbit.

In conclusion, wa can check if our companies has parity or not by asking a single question to HR.

Takeaways

• Deutsch algorithm proves that Quantum algorithm can decrease the number of queries required to solve a problem.
• The \(\oplus\) operator is use to create Quantum entanglement, when the value of a qbit depend on the value of another qbit.
• By using entanglement, we can use information of other qbits without having to measure them.