An introduction to Quantum Processing - The QBit

I don't like deep learning and current AI buzz. Really. That "Hey, let's initialize billions of values and make them converge to whatever good enough solution could solve some problem with good probability, but we don't know how" really annoys me. So I decided to take a look at the next breakthrough technology before it becomes a buzzword: Quantum Computing.

Classical computers use bits. Quantum computers use qbits. That's it, end of the discussion.

Just kidding...

Quantum Superposition

First, let's talk about some properties of Quantum space:  the Quantum superposition. In classical computing, the value of a bit is either 0 or 1. Light is on or off. Gate is open or closed, etc...

In quantum computing, the value of a qbit is undefined until we measure it. You can imagine the qbit oscillating very quickly between 0 and 1, but when you take a measure, it stops where it was when it was. Let's assume the qbit flipping from 1 to 0 every millisecond. Then, you measure it by pressing a button. You have a 50% chance of measuring it to 1 and a 50% chance of measuring it to 0.

Now, imagine a qbit staying 3 ms in 1 state and 1 ms in 0 state. When you measure it, you have a 25% chance of measuring 0 and a 75% chance of measuring 1.

This “oscillation” is called quantum superposition. You can also imagine the qbit having both values at the same time if you prefer. We call this the quantum state of the qbit.

— So it has 2 states in once ?

Not really. Qbit has only one quantum state. But when we measure it, it will be either 0, either 1.

In classical physics, the state of a system is equivalent to its value. If your car is moving at 100 km/h and a police officer measures its speed, he will get 100km/h.

In quantum mechanics, the quantum state of a particle is not equivalent to its measure. The particle is in a superposition state, which can be described as "50% 0, 50% 1". But when we measure it, we won't have something like 0.5. We have either 0 or 1. And the crazy thing is the qbit then keeps this value after the measure. Meaning several values in a row will all give the same value.

— But how is this possible? How can measuring something have an impact on this thing? I didn't touch the qbit, I've just watched it !

Yes, yet another fun thing about quantum mechanics. Seeing something actually change its state. You can imagine that, to see something, you have to light it, and see what effect this object has on light. You have to see its interaction with photons. Generally speaking, measuring something means measuring how this thing impacts its environment. In human scale, this would be similar to throw a rock at someone and see how the rock is deviated. You will for sure change the state of the specimen. But we are getting off topic; let's go back to our qbits.

Vector representation

To represent the qbit state, we can use Vector representation.

Let's assume a vector ψ [α, β] of unit length:

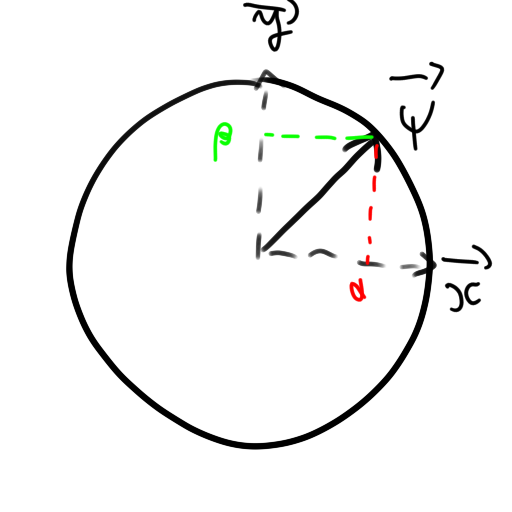
We know that α² + β² = 1. In the case above, α=β=1/√2.

We can represent a qbit ψ the same way, using a slightly different notation convention called Bra-Ket notation :

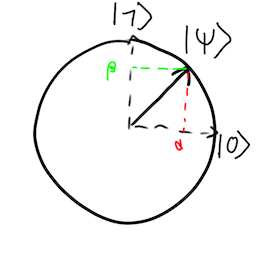
One pronounces |0⟩ "Ket zeros", |1⟩ "Ket one", |ψ⟩ "Ket Phi", etc...

Using Cartesian coordinates, these vectors respectively have coordinates

• |0⟩: [1, 0]
• |1⟩: [0, 1]
• |ψ⟩: [α, β]

α and β represent the probability of measuring a qbit in the value 0 or 1. More precisely, probabilities are respectively p(0)=α² and p(1)=β², so that p(0)+p(1)=1.

We end up with p(0)=1/(√2)²=1/2. So, there is a 50% chance of having 0 when measuring a qbit. Same for 1.

Any qbit |ψ⟩ can be expressed as a superposition of values |0⟩ and |1⟩ using the formula:

|ψ⟩ = α|0⟩ + β|1⟩

The Bloch sphere

The subtlety is that α and β are actually complex numbers. So |ψ⟩ is actually described using 4 real numbers a, b, c, and d:

|ψ⟩ = α|0⟩ + β|1⟩ α, β ∈ ℂ ⇔ |ψ⟩ = (a+b*i) |0⟩ + (c+d*i)β|1⟩ a, b, c, d ∈ ℝ

Complex numbers can also be written as r e^iθ, so:

|ψ⟩ = r_α e^iθ_α|0⟩ + r_β e^iθ_β|1⟩

However, in quantum mechanics, only the relative phase between α and β has any physical meaning. Only ^{θ_β - θ_α} is important. We can offset the phase so that θ_α = 0 and have

|ψ⟩ = r_α |0⟩ + r_β e^iθ_β|1⟩ = α|0⟩ + β|1⟩ with α ∈ ℝ, α > 0, and β ∈ ℂ.

|ψ⟩ can now be perfectly described with 3 real values. We also know that |ψ⟩ has unit length. This gives us another constrains:

∥|ψ⟩∥² = ∥r_α |0⟩ + r_β e^iθ_β|1⟩∥²

r_α² + r_β² = 1

Among all the trigonometric equations you have learned at school, there is a one saying:

cos(θ)² + sin(θ)² = 1

Let's define θ so that r_α = cos(θ/2) and r_β = sin(θ/2) which satisfies this constrains.

— Wait, why not cos(θ) ?

Because Math hates you.

So, we finally reach the final forms of the equation:

|ψ⟩ = cos(θ/2) |0⟩ + sin(θ/2) e^iϕ |1⟩

And ended up with only 2 real parameters, θ and ψ, where 0 ≤ θ ≤ π and 0 ≤ ϕ \< 2π. But contrary to the first Cartesian representation, the quantum state of |ψ⟩ is now perfectly described.

To visualize this new representation, we can interpret ϕ and θ as azimuth and elevation angles:

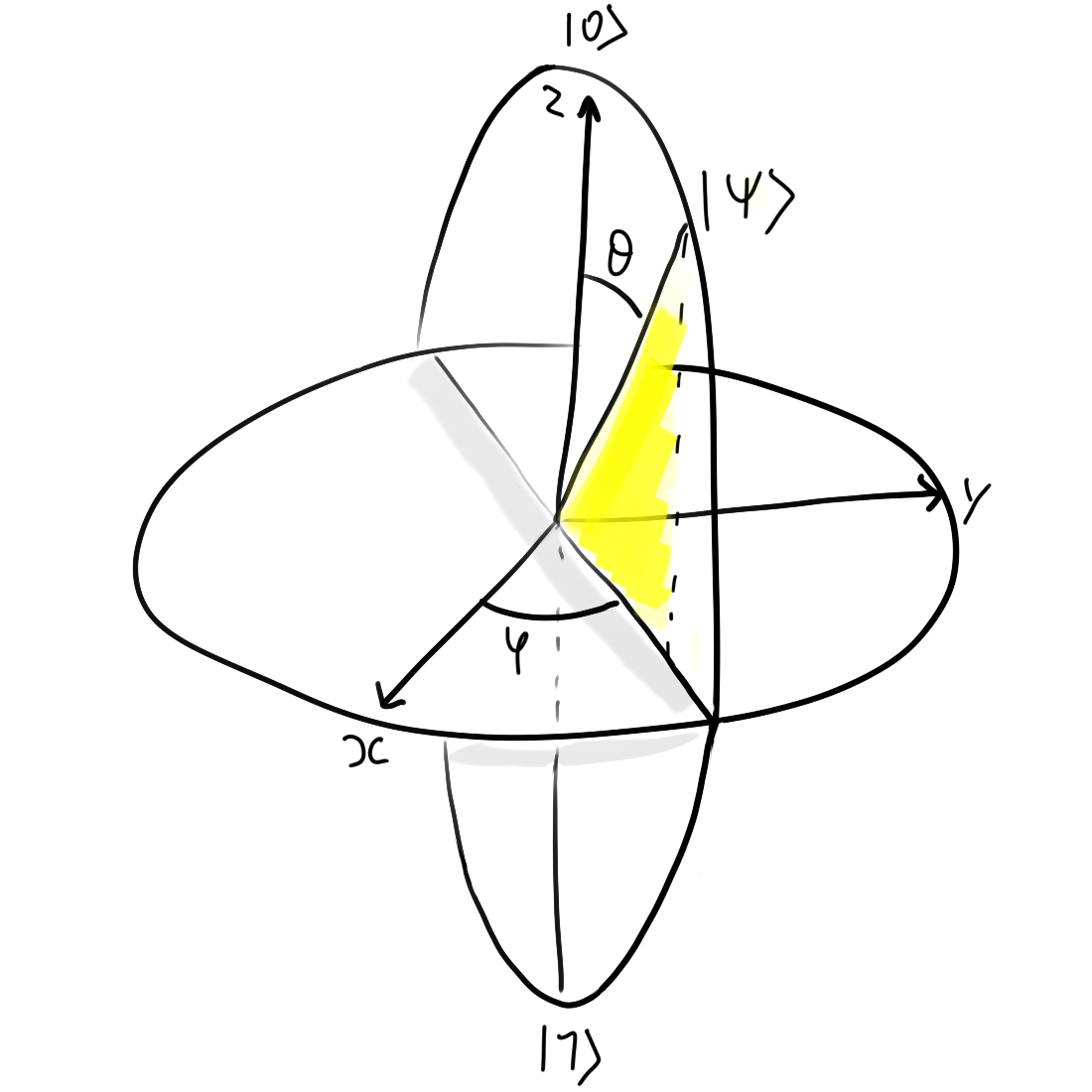
This sphere is called the Bloch sphere. And one can notice that when θ=0, |ψ⟩=|0⟩, and when θ=π, |ψ⟩=|0⟩, which also correspond to cartesian representation from previous section, modulo a 1/2 factor on θ.

— So, couldn't we call it the Bloch Hemisphere and get rid of the /2 factor ?

No, we can't. 😠

Takeaways

• In classical computing, a bit ψ has value 0 or 1, which correspond to its current state.
• In quantum computing, a qbit |ψ⟩ has an infinite of possible state which are combination of |0⟩ and |1⟩. But when measuring it, its value will be either |0⟩ or |1⟩.
• The probability to have |0⟩ or |1⟩ when measuring |ψ⟩ is respectively equal to α² and β².